Self-Balancing Inverted Pendulum - Project Execution and Demo

25 Aug 2020

Introduction

In the final installment of the Self-Balancing Inverted Pendulum series, we will be covering the controller design for the robot constructed through the previous posts in this series. We will also be demoing the operation of the robot, once the Arduino code has been loaded onto the robot.


Final Controller Tuning

In the first post of this series, we saw how Matlab can be used to generate the controller state gains required to create a closed-loop inverted pendulum system. In the third post, we measured the parameters that are fed into the Matlab model. We are now at a stage where we can complete the final tuning of the robot. Generation of the controller state gains is a simple process of copying in the information from the third post into the code supplied in the first post. Shown below is the code used to generate these gains based on the physical measurements made on the robot. 


M = 0.316; % mass of cart in kg
m = 0.334; % mass of pendulum in kg
b = 0.1; % coefficient of friction experienced by cart
I = 0.00386; % moment of inertia of pendulum in kg.m^2
g = 9.8;
l = 0.123; % length to pendulum center of mass in m

p = I*(M+m)+M*m*l^2;

A = [0      1              0           0;
     0 -(I+m*l^2)*b/p  (m^2*g*l^2)/p   0;
     0      0              0           1;
     0 -(m*l*b)/p       m*g*l*(M+m)/p  0];
B = [     0; (I+m*l^2)/p; 0; m*l/p];
C = [1 0 0 0; 0 0 1 0];
D = [0; 0];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'u'};
outputs = {'x'; 'phi'};

sys_ss = ss(A,B,C,D, 'statename',states, 'inputname',inputs, 'outputname',outputs);

Ts = 15/1000;

sys_d = c2d(sys_ss,Ts,'zoh')

co = ctrb(sys_d);
ob = obsv(sys_d);

controllability = rank(co)
observability = rank(ob)

A = sys_d.a;
B = sys_d.b;
C = sys_d.c;
D = sys_d.d;
Q = C'*C
Q(1,1) = 5000;
Q(3,3) = 100;
R = 1;
[K] = dlqr(A,B,Q,R)

Ac = [(A-B*K)];
Bc = [B];
Cc = [C];
Dc = [D];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'r'};
outputs = {'x'; 'phi'};

Nbar = -55.55;
sys_cl = ss(Ac,Bc*Nbar,Cc,Dc,Ts, 'statename',states, 'inputname',inputs, 'outputname',outputs);

t = 0:0.015:5;
r =0.2*ones(size(t));
[y,t,x]=lsim(sys_cl,r,t);
[AX,H1,H2] = plotyy(t,y(:,1), t,y(:,2), 'plot');

set(get(AX(1),'Ylabel'), 'String', 'cart position (m)')
set(get(AX(2),'Ylabel'), 'String', 'pendulum angle (radians)')
title('Step Response with Digital LQR Control and Precompensation')

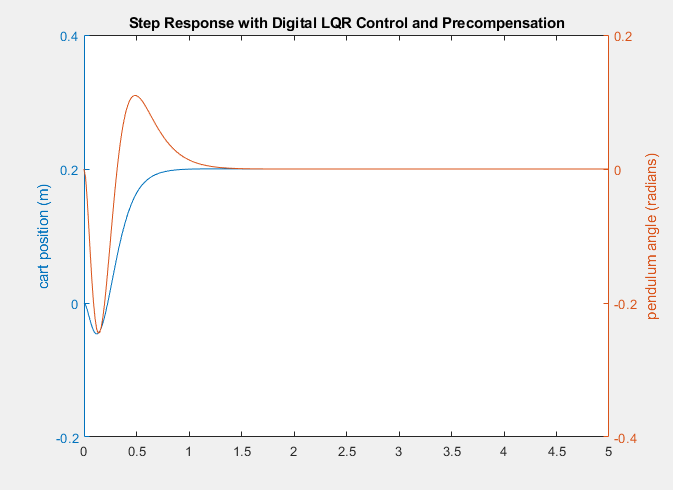
After running the code, the plot shown in Figure 1 should appear. Controller state gains, the K vector, should also be printed to the terminal as [-55.5460, -23.9438, 56.5291, 8.0602] where each value corresponds to [cart position, cart velocity, pendulum angle, pendulum velocity], respectively. As in the original simulation, we are still tuning the controller by using a 0.2 m step function. The specific response of the simulation is somewhat redundant since the original objectives of the robot do not specify a specific response time or response characteristic. Additionally, unless your system is setup to control the current being fed to the motors, there is no way to reliably control the force delivered by the motors. Instead we use the response in Figure 1 to verify that the system is stable, and then use the ratio of K values outputted in the terminal as a basis for the magnitudes of the four states as they will be measured on the Arduino.

Figure 1 - Final controller tuning simulation output.

Once Arduino code has been developed (example MPU-6050 code can be added to your Arduino library and you can work off this to add the rest of the systems functionality!), the K matrix values can be subbed in and the final tuning process can begin! Since we are not using the values to specify the force applied to the motors, there is a little bit of manual work involved here. To get the motors to apply enough force to balance the pendulum, I simply multiplied the K vector by a constant of increasing value until it was able to balance. For this specific case, the constant value I found to work best was 10. Then to clean up most of the jerking behaviour and allow the robot to operate a little smoother, I reduced the multiplier on the pendulum derivative by 40% and reduced the multiplier on the cart position and cart velocity states by 10%.

Specifically, on the Arduino the process would take the following form:

  1. Measure current value of all four states
  2. Multiply the K vector by the multiplier vector
  3. Multiply the new K vector by current value of all the state vector
  4. Convert force output value to PWM value
  5. Send command to motors

Note that the conversion from the force output is really just assigning the force output specified by the controller as the PWM value to be sent to the motors. Without the tuning of the multiplier vector, this conversion is completely meaningless since you cannot control motor force with PWM alone. The tuning of the multiplier vector allows the conversion to gain meaning within the context of the system such that measuring the current states of the system at each time step will enable an appropriate PWM value to be identified and sent to the motors.


Self-Balancing Inverted Pendulum Demo

After the final tuning was complete, the inverted pendulum robot was finished. I created a YouTube video to demo the operation of the robot. See the link below!


Future Improvements

While the robot achieves all of the objectives outlined in the original post of this series, there are still some improvements that could be made. For one, under optimal control, the inverted pendulum would look like the robot is not moving at all when no external disturbances are applied. Due to the brushed DC motors used in this robot, this is unfortunately not possible. Friction from the carbon brushes on the rotor of the gearmotors prevents small movements from occurring until enough current is flowing through the motor windings to overcome this friction force. In a future version of this robot, the brushed gearmotors should be replaced with either brushless DC motors or servomotors so that these small adjustments can be made on the pendulum.

The last improvement I would like to make is to include a power pack on the robot to provide power to the motors directly rather than use a power tether, as can be seen in the video. A self-contained power source for the motors will make the robot even more mobile as well as make it easier to demo the robot in different locations where a mains connection may not be available.

If you've followed through this series as I walked through the construction of the self-balancing inverted pendulum, I want to say thank you for viewing my work and I hope you enjoyed reading it! Look forward to more hobbyist posts to come in the future!